In the previous post we attempted to price a vanilla European option using the QuantLib and Boost libraries. We almost got the program to run as we successfully defined the option parameters (like Spot, Strike, Volatility etc…) using QuantLib’s data types, and we even used Boost’s shared pointers to create sophisticated objects with particular QuantLib types knowing full well that the creation and destruction processes would be handled automatically.
However when we went to price the option the code fell over because the Instrument object was expecting a Pricing Engine and we had given it none.
Pricing Engine
QuantLib provides many kinds of pricing engines. As the name suggests, we will be using QuantLib’s Analytic European Engine. This means that it will try to use known closed-form, or analytical solutions – perfect for pricing vanilla European options!
Peeking at the class header we see that in order to instantiate such an object we need to give it a stochastic process.
Stochastic Process
The engine class constructor requires us to provide it a type, not just any type, but a Boost Shared Pointer type (which is a template for a type) and the passed-in type will then become the underlying stochastic process upon which the pricing engine will run.
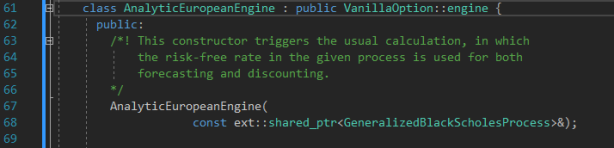
Let us make the decision to use a 1-dimensional Geometric Brownian Motion to price our European option – this is the standard stochastic process assumption to make (not always the best choice, but for a vanilla European option it is probably the best). Let us call our process variable bsmProcess and declare it in the following way:
QuantLib::BlackScholesMertonProcess bsmProcess();
This declaration is close but it won’t quite work. Two things: remember, the Pricing Engine is expecting a pointer to a process, and QuantLib’s BSM process object has an overloaded constructor, one of which requires us to pass in several arguments, oh no… We can see this fact by peeking at the class header for the BSM process:
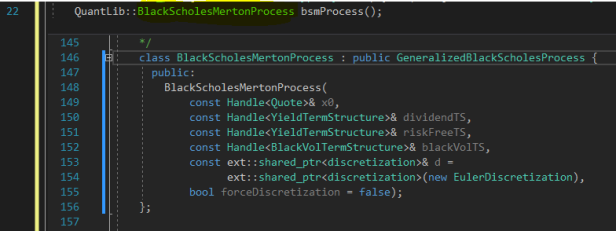
Thus, in order for us to create a stochastic process to feed the pricing engine, we need to tell the stochastic process object exactly how to create itself by supplying
- Initial value,
- Dividend curve,
- Risk Free Interest Rate curve,
- Volatility surface,
- Time steps
That’s a lot of parameters! Luckily QuantLib provides an object that contains all of these parameters…the term structure object.
Furthermore, since the bsmProcess() variable will need to be declared (like the others) with a new object (yet to be discussed) we need to again wrap it’s type in the Shared Pointer syntax like so:
boost::shared_ptr bsmProcess(new [Object]);
As a rule of thumb, whenever the variable being declared requires a new object to be input as an argument, one should wrap the type with a shared pointer.
The Term Structure Object
The BSM process object requires a term structure of interest rates (or just term structure or a time-dependent curve or surface) to be supplied to it when it is created. So let’s create the most simple term structure object, a.k.a. a flat term structure:
QuantLib::BlackScholesMertonProcess(spotPrice, flatDividendTS, flatTermStructure, flatVolTS);
Now we have to tell it what all the flat term structure (TS) components are. Peeking once again we get a clue as to what data types they will be. They will be constant QuantLib Handles, so we proceed with:
QuantLib::Handle spotPrice();
But this won’t work either…. Here’s why:
The Spot Rate and Abstract Base Classes
While Quote is the correct type, and the type that the Stochastic Process object is expecting (see image above), QuantLib’s Quote class is actually an abstract base class. This means (among other things) that all of it’s member functions are virtual, i.e. they are not defined! Where are they defined then, you may ask? In the classes that inherit that class.
This means that while we have to define spotPrice as a Quote type, in order to get values in to that object, we need to also instantiate one of the inherited, non-abstract class objects. OK, so what inherits Quote? SimpleQuote does:
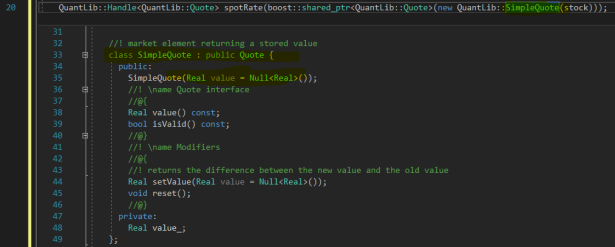
As you can see, SimpleQuote inherits from the abstract base class Quote. Furthermore, it’s constructor takes in a real number (a.k.a. the Spot Price). Perfect. Let’s use it! To implement the spotPrice for use in the Term Structure object we declare the following:
QuantLib::Handle<> spotPrice(boost::shared_ptr(new QuantLib::SimpleQuote(stock)));
So when spotPrice is created, it creates the inherited class object SimpleQuote and takes in the stock price value as a Real object.
The Other Term Structure Objects
Using the Peek function can we quickly declare the remaining three variables we need?
QuantLib::Handle flatDividendTS(); QuantLib::Handle flatTS(); QuantLib::Handle flatVolTS();
Unfortunately, no. The Yield Term Structure and the Black Volatility Structure requires even more objects to be passed in! Let’s take a look at what we need to do:
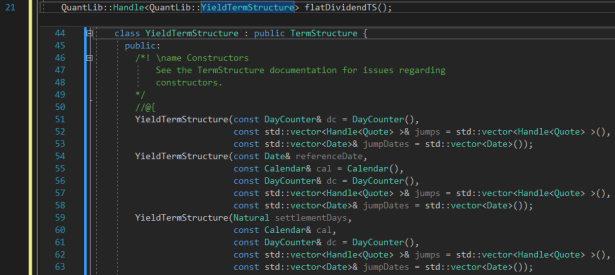
OK, so we need to provide it with a DayCounter, and Jump Dates. Erm… How do we do that? I had to cheat here because I had no idea. Either I would have to declare each and every argument required for the constructor, or hopefully, QuantLib had yet another object that could handle all of these.
Some Googling and it turns out that the QuantLib object called FlatForward handles these objects for a Flat Term Structure assumption (if we had not wanted a flat term structure, this would be much more difficult to describe).
So let’s create the FlatForward object when the Flat Term Structure variables are created inside a Boost Shared Pointer like so:

Ah, didn’t quite work. Not as easy as I thought. Turns out that the FlatForward object also requires input arguments upon construction. Let’s Peek:
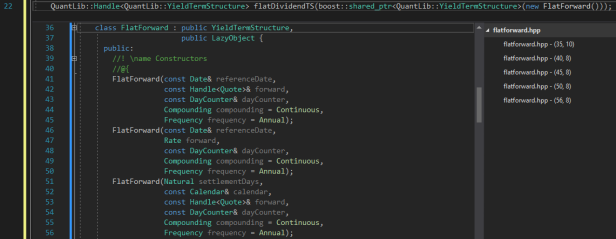
OK, this looks good. Seems we have to declare five inputs, and two of those have defaults (gotta love defaults). So all we need to do is pass in a Reference Date, a (forward) rate (but since it’s flat we can provide spot), and a DayCounter and we will be good!
The DayCounter Object
Luckily, QuantLib has thought of everything, and it also has a DayCounter data type! Let’s go back to the top and add a DayCounter variable in and set it equal to the usual Actual 365 Fixed:
QuantLib::DayCounter dayCounter = QuantLib::Actual365Fixed();
Let’s also supply the FlatForward object with our already created variables settlementDate for the ReferenceDate and the dividendYield for the forward argument:

Hurrah! It works.
So now we have defined a flat dividend term structure by creating a QuantLib YieldTermStructure data type and passing in a FlatForward object which creates a term structure of prices out of the spot Dividend rate and extrapolates from the Settlement Date out to Maturity (by default) along the Actual 365 Day Count Convention. It’s all handled by QuantLib! Normally, defining term structures is about 50% of the pricing model job, and they’re incredibly annoying and tedious. Doing it this way (at least for our flat term structure environment) it is very easy. You’ve just got to be patient and keep peeking at the class headers for clues as to what is required to be passed in to each object upon instantiation (or variable creation). Keeping in mind that it is always a good idea to wrap the data type with Boost’s shared pointer any time the variable declaration requires another object to be created (i.e. with the new keyword).
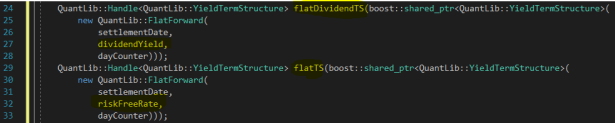
Look how easy it is to create the same flat term structure objects except one is of the dividend yield and one is of the risk free interest rate:
The Black Volatility Term Structure
What about a flat volatility surface? Well, not because we wanted to be a bit more tricky with the vol surface, but the class constructor demands a new type of input.
Upon peeking the class header we see that it is very similar to the FlatForward object except that we also need to provide a calendar. Luckily we already have defined a calendar, so here we go:
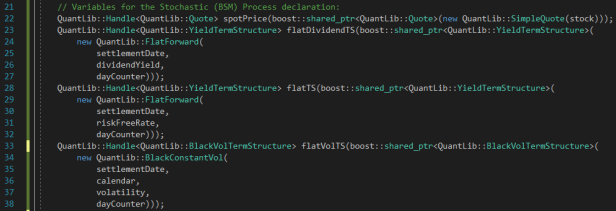
Where did BlackConstantVol come from? The Internet. I googled QuantLib for the required object…. See here for an example.
And now the bsmProcess variable can be declared and also passed in to the Analytic European Engine:

Full Listing of Test.cpp
#include <iostream>
#include <ql/quantlib.hpp>
#include <boost/shared_ptr.hpp>
int main(int, char*[])
{
// Date Stuff
QuantLib::Calendar calendar = QuantLib::TARGET();
QuantLib::Date todaysDate(6, QuantLib::December, 2018);
QuantLib::Date settlementDate(6, QuantLib::December, 2018);
QuantLib::Date maturity(6, QuantLib::December, 2019);
QuantLib::DayCounter dayCounter = QuantLib::Actual365Fixed();
// Initial Values
QuantLib::Option::Type OptionType(QuantLib::Option::Call);
QuantLib::Real stock = 100.00;
QuantLib::Real strike = 90.00;
QuantLib::Spread dividendYield = 0.00;
QuantLib::Rate riskFreeRate = 0.05;
QuantLib::Volatility volatility = 0.20;
// Creation of Exercise and Payoff objects:
boost::shared_ptr<QuantLib::Exercise> europeanExercise(new QuantLib::EuropeanExercise(maturity));
boost::shared_ptr<QuantLib::StrikedTypePayoff> payoff(new QuantLib::PlainVanillaPayoff(OptionType, strike));
// Create the European Option (Instrument) object:
QuantLib::VanillaOption europeanOption(payoff, europeanExercise);
// Variable Handles for the Stochastic (BSM) Process declaration (incuding Flat Term Structures):
QuantLib::Handle<QuantLib::Quote> spotPrice(boost::shared_ptr<QuantLib::Quote>(new QuantLib::SimpleQuote(stock)));
QuantLib::Handle<QuantLib::YieldTermStructure> flatDividendTS(boost::shared_ptr<QuantLib::YieldTermStructure>(
new QuantLib::FlatForward(
settlementDate,
dividendYield,
dayCounter)));
QuantLib::Handle<QuantLib::YieldTermStructure> flatTS(boost::shared_ptr<QuantLib::YieldTermStructure>(
new QuantLib::FlatForward(
settlementDate,
riskFreeRate,
dayCounter)));
QuantLib::Handle<QuantLib::BlackVolTermStructure> flatVolTS(boost::shared_ptr<QuantLib::BlackVolTermStructure>(
new QuantLib::BlackConstantVol(
settlementDate,
calendar,
volatility,
dayCounter)));
// Creation of the Underlying (1-d) Stochastic Process:
boost::shared_ptr<QuantLib::BlackScholesMertonProcess> bsmProcess(new QuantLib::BlackScholesMertonProcess(
spotPrice,
flatDividendTS,
flatTS,
flatVolTS));
// Creation of the Pricing Engine:
boost::shared_ptr<QuantLib::PricingEngine> Engine(new QuantLib::AnalyticEuropeanEngine(bsmProcess));
// Set the Pricing Engine:
europeanOption.setPricingEngine(Engine);
// Output Results:
std::cout << "Option Start Date = " << todaysDate << std::endl;
std::cout << "Option Settlement Date = " << settlementDate << std::endl;
std::cout << "Option Maturity Date = " << maturity << std::endl;
std::cout << "Option Type = " << OptionType << std::endl;
std::cout << "Stock Price = " << stock << std::endl;
std::cout << "Strike Price = " << strike << std::endl;
std::cout << "Risk Free Rate = " << riskFreeRate << std::endl;
std::cout << "Dividend Yield = " << dividendYield << std::endl;
std::cout << "Volatility = " << volatility << std::endl;
std::cout << "European Option Price = " << europeanOption.NPV() << std::endl;
return 0;
}
Summary
In this post we introduced QuantLib’s Pricing Engine object and used it to price a vanilla European option by setting it up with an underlying, 1-dimensional geometric Brownian motion (BlackScholesMertonProcess) and passing it to the Instrument object.
We discovered that there are several pricing engines and stochastic processes to choose from. Further, we discovered that the term structure of interest rates (YieldTermStructure) is a crucial ingredient in setting up these instruments. These can get quite complex so we used QuantLib’s flat term structure object (FlatForward) to bypass a lot of intricacy.
We encountered our first example of having to instantiate an inherited class (SimpleQuote) because the type required by a constructor was an abstract class (Quote).
