In this last article we attempted to motivate the use of the Quantum Fourier Transform (QFT) in a quantum circuit by looking at what happens when we assume:
- a unitary operator, and
- exactly
qubits
Then we could then factor the unitary operator as
We then extended the unitary operator in to a controlled unitary and noticed that it has the exact same form as the controlled phase gate which essentially maps
to
, i.e. rotates the
state counter-clockwise about the unit circle in the complex plane.
With the Hadamard gate and the controlled phase gates
we could then apply a sequence of them to build the following quantum state:
which is nothing but:
which is the mathematical represention of the discrete Fourier transform!
Then, in this article, we derived the actual matrix representation of the QFT. Here is what it looks like for a resgister of 4 qubits:
Notice that the first row and the first column are filled with 1’s? This is always the case for the QFT of any dimension; a property which is very often utilised in linear algebra calculations.
So how do we use this?
Well, let’s say that we have two quantum registers that differ only in their relative positions. We indicate this by permuting the indices of the individual qubits:
Now look what happens when we apply the QFT to them:
and
All the indices line up again!!!
The difference between the two outputs crucially only differs by a relative phase shift (see the ordering of the ‘s is
in both cases, but some of the qubits have picked up a bit of phase, that is to say, some of the qubits have rotated a little bit), which makes absolutely no impact on the measurement of the register.
The phase of the state does not effect the probability of measuring that state.
As another illustrative example, imagine that we have the following two physically identical states:
What do you think will happen to these qubits?
It turns out that, even though they are physically identical, the application of the QFT on each of these does result in different outputs!
What on Earth is going on!?
Somehow we can have two physically identical states but physically different Fourier transformed states. While also having two physically different states but physically identical Fourier transformed states.
Confused?
It appears that the QFT is sensitive to some hidden characteristics of a register of qubits, while being completely indifferent to others.
We will exploit this behaviour of the QFT in what follows. But we will also need to know what are these characteristics.
The Algorithm
So how can an algorithm find prime factors?
Well, there are many classical algorithms which do the job just fine (although slowly) and they’ve been around for a long time. For example, the quadratic sieve or the general number field sieve (the fastest known classical algorithm), which uses a few simplifying assumptions (like is composite and odd, the Euclidean algorithm, the fundamental theorem of arithmetic, and the Chinese remainder theorem, etc…) to speed things up. But they are all essentially implementing the greatest common divisor (GCD) function that spits out the list of prime factors as you choose different, randomly chosen starting points, denoted
.
These are all classical algorithms – and not the subject of this article. Suffice it to say: those algorithms are all very well known and work rather well. I would say that the only weakness in the classical algorithms is in the subroutine that attempts the find the period of the function , where
is the random choice that the algorithm makes in its first step that attempts to preclude it from potential divisors of
.
The faster the algorithm can preclude more and more ‘s the faster it can narrow down non-trivial factors of
, leaving just the best candidates for prime factors. But it still has to randomly choose a starting point
and decide if it satisfies as being a prime factor or not.
Thus, if the algorithm finds out that then it knows that
results in a non-trivial factor and we can exclude it. However, if it finds that
(i.e. a trivial factor) then
only might be a prime factor and further testing must be done.
This further testing is when we need to figure out the period of
If it turns out that the period is odd then the chosen at random is no-good. However if it is even then there is a good chance it is good (just one more classical test is required).
It is in the figuring out the order of this periodic function where the quantum Fourier transform comes in. Everything else, stays classical.
Using the QFT to Find the Order of a Periodic Function
So, how does the QFT help us find the period of a periodic function?
First, note that there are many ways to factor an integer besides reducing factoring to period-finding.
In the last section above we showed that we can easily find a factor of given the order of some element. What remains is how do we determine the order? Because, if we know the order we can exclude the test if it is odd and move on to the next test; greatly speeding up the algorithm.
Classical computers suffer badly when trying to figure out the order of a function because they have to check each candidate one after the other until a success is found.
Even and Odd Functions
All right, let’s step back for a second and recall what even and odd functions are.
Two things can happen when you try to compute a shift in the argument of a function: . Either
, like, for example, when you add 360 degrees to the argument of a sine function:
) and we say that it is periodic. Or,
doesn’t equal itself, and it instead equals some difference or remainder, which can be expressed as a remainder in some modulus:
and we say that it is not periodic.
Further, if the function is periodic and then we call the periodic function even and there will be symmetry about
. They are called even because the first such functions discovered that display this property were of the type
, where
is an even integer. However, not all even exponents result in an even function. For example,
is not even.
A function is odd if it changes sign when the argument is negative: and there will again be symmetry about
. For example, the cosine function is even while the sine function is odd.
Even and Odd do not cover all examples of periodic functions. There are a huge number of functions which are neither even nor odd. Yet, it is very easy to test if a function is even or odd: just substitute for
in the function argument and see what you get. If the negative sign works its way through and ends up out the front then you have an odd function. If it works its way through and cancels with itself leaving the original function as though you had put a positive argument in, then you have an even function. If you get some ugly mess, then you have neither.
Primitive Roots of Unity
The last tool we need in our toolbox is the concept of a primitive root of unity. Recall that with the complex numbers there always exists solutions to the simple equation
For example, if , the complex number
would be
or
. If
, then
. But these are just points on the unit circle in the complex plane. We know an equivalent expression for points on the unit circle:
As such, it is much easier to write the solutions for as simply
where
runs from 1 through to 4, in this example. So we don’t need to actually calculate the solutions to
, we simply use the
function (the so-called primitive root of unity) at each
to find the full set of solutions.
In this language, when , then the solutions are simply
and we are done.
If you want to know specifically what, say, is, then you would have to evaluate it:
Graphically, these solutions all lie on the unit circle (hence the name):
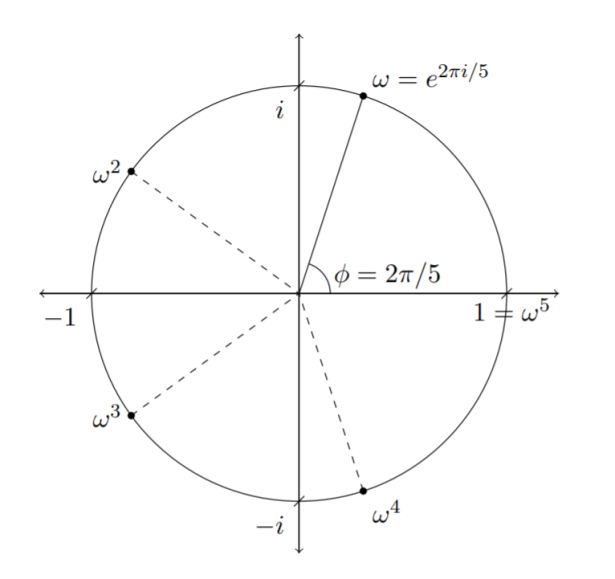
and they are all equally spaced apart.
The Discrete Fourier Transform
We’ve already seen in past articles that the QFT can be written in matrix form for any dimension as:
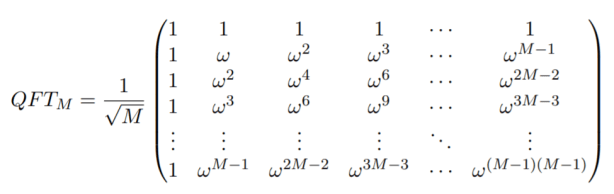
The 2-dimensional QFT (i.e. with ) becomes
But since , we have that
is just the 2-dimensional Hadamard gate!
Indeed, the QFT is a generalisation of the Hadamard gate.
The QFT is also unitary because its columns are all pairwise orthonormal. This also means that whenever you perform the QFT and then its adjoint, you get the identity operator:
Period Finding
What is period finding?
Well, suppose you have a periodic function (e.g. ), that is, some function which repeats itself for larger and larger input values. For example, the sine of
is periodic because when
,
which is that same value as when
. In other words,
for all integer multiples of
.
But what if I said that ?
No it doesn’t…
Oh, but it does… in modulo .
In fact, all of those ‘s that render the sine function zero are all equal to each other…in modulo
.
Periodic functions and arguments equalling one another in some modulo are equivalent statements:
A periodic function has the property that
if and only if
In our case, the remainder was just
. But in general, we don’t know that
is periodic…until we find
, the so-called period, then we know.
We can already classically find the period by checking precisely every single value that it could be…that’s
number of checks.
Very slow.
In fact, as the dimensionality increases, the number of checks is
, and so we say that finding the period classically is a problem in exponential time. One of the slowest, if not, the slowest types of problems. That’s not good. And it is this slowness which ensures the robustness of classical public-key cryptography.
With quantum computers though, we can place functions in superposition and query the values in just
checks. A so-called exponential speedup. Here’s how:
If we take our register of qubits, initialised in the zero state, we can place the first
in superposition, with an application of an
-sized QFT (a.k.a. Hadamard):
Now, we transform our ancilliary zero-state according to some unitary operator which essentially performs the evaluation of the function
:
If we then decide to measure the ancilliary state , it must collapse in to some measureable value
. Furthermore, since measuring
reveals some information about
, the QFT state
must also collapse in to the pre-image of
.
But that’s not so bad, because we know that is periodic.
Which means the pre-image must contain some set of periodic values:
So, our measurement makes this change:
The astute reader will notice that the summation has narrowed, and we will be just ignoring the last bits, essentially they have been fixed by the measurement.
Now our register is in a periodic superposition where its period is equal to the period of the function .
But we can’t measure it just yet! This is because when we run this algorithm up to this point we might measure a different value of , thus obtaining a periodic superposition that’s linearly shifted, and this random shift relays back useless information.
The QFT again comes to our rescue.
Recall that if a function is periodic with period
such that
, then the Fourier transform
will also be periodic but with a period
. The QFT naturally extracts the period.
Further, recall that when this happens, any constant linear shift inherent in the function is transformed in to the phase of .
The Quantum Fourier Transform not only transforms periods of the form
to
, but also transforms constant shifts in to the phase. This enables us to extract the period without physically affecting the qubits doing the operation.
Therefore, if we take the QFT of the first register, we will be left with only the states that are multiples of . This is all in Section 5.3 of [2].
Applying the QFT again to the first bits we get (as in [5]):
where is just some, unimportant phase associated with each term due to the linear shift. Sometimes it is denoted by
.
We can now measure and retrieve for some integer
.
We repeat this algorithm and measure to retrieve several multiples of . Once we have enough values we can compute their GCD (thanks to Euclid’s Algorithm) to retrieve
. And since
is known,
is easy to deduce.
This algorithm can be summed up by the following circuit:
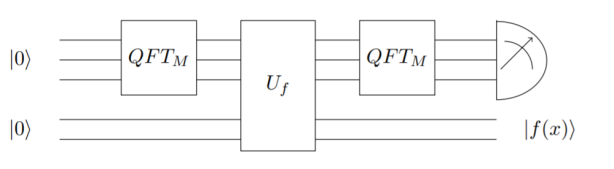
Example
OK, I understand all of that was pretty high-brow, and probably didn’t make a whole lot of sense. So let us go through a concrete example.
Suppose we define a periodic function to be equal to
. In this case, we know beforehand that the period is 2. But let’s just pretend that we don’t know this, and see if we can find the same value using the above quantum algorithm.
Let’s use a 3-qubit system, so that , but really, as we know, any power of two will work. We could use any size, but for the convenience of the math, let’s keep to it
.
First, let’s apply the QFT. The QFT of 3 qubits is the QFT matrix, thus:
Now we apply our unitary function:
Before continuing, let is peek inside and see what the state looks like:
OK, so that is interesting. All those qubit states are odd. Measuring this state of this register will yield a 1, 3, 5 or 7 with equal probability of 25%. So a sequence of measurements might look like this: 31755713357137735731355753135753137771573573171735… which is just a random sequence of integers. How do we get the number 2 from this?
Well, we can’t just yet. So we once again apply the QFT:
Note: if instead of measuring we had measured
, there would be a different linear shift. But the properties of the QFT dictates that this only affects the phase of the Fourier transformed function. In other words:
See how the answer is still !? We’ve seen this before, we we saw that the QFT sometimes returns the exact same state even though different states were inputted. This is one of those cases!
So now we are getting somewhere. Now, no matter what the function is, if we apply the QFT and then the inverse QFT we get this state back. And now, finally, if we take a few measurements of this state we will see varying amounts of
and
, and nothing else. So a sample result set might look like: 00044040440440400400404…
Now we definitely can extract the number 2 from this.
Taking the largest value (which is 4) we can solve the equation , and since we know that
from our qubit register setup, it is clear that the period of
is
.
In this case, was a multiple of
(i.e. a multiple of
. When this is the case (and it definitely is not always the case – depending on the basis), then
and so the coefficient was .
It should be clear by now that we get this coeffcient due to the constructive interference in rotations around the unit circle. When is not a multiple of
, we get destructive interference. This interference that we get is one reason why quantum computers are so well-equipped for period finding.
Additions in the phase of the qubit state create constructive and destructive interference, cancelling and enhancing the probabilities of observing the correct quantum state upon measurement after performing a quantum Fourier transform.
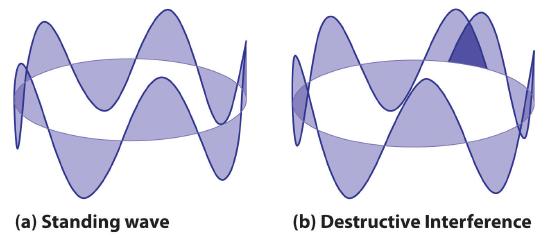
Summary
We saw how a QFT is sensitive to the phase-structure of a register of qubits. Just because a register of qubits is physically identical to another is not enough to ensure the QFT of those registers will be identical. Small differences is the unobservable, unphysical global phases can wildly affect the outcome of the QFT. But by the same token, some states will be identical under a QFT, and we took advantage of this when we mapped the different result sets of to the same state
We then found a way to programmatically turn a function in to a binary test, by determining whether or not it is an even or an odd function – a binary outcome.
Then we found a connection between the primitive roots of unity and the matrix elements that make up the unitary QFT. We saw that the simplest QFT is, in fact, just the Hadamard transform. Higher-dimensional QFTs are just unitary matrices of rotations in the complex plane, just as products of primitive roots of unity are.
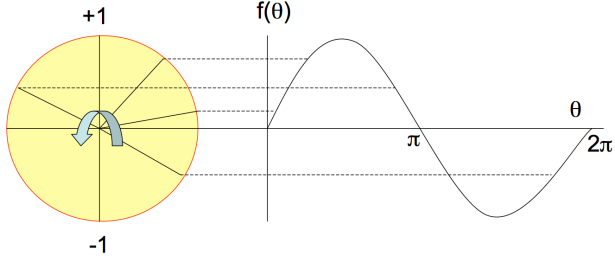
We then came to the problem of period finding. By first placing a register of qubits in to a superposition (via a QFT as a generalised Hadamard), we then apply the periodic function whose period we seek as a unitary transformation on the superpositioned register of qubits. By the definition of periodic, if we make a measurement here, we know the qubit states must collapse in to one of the periodic values, but not necessarily the largest one that we seek. We can increase the probability of finding the right one by applying the QFT again (and in this case, not necessarily as a Hadamard but as a way to provide destructive and constructive interference in the global phases of the superpositioned qubits, so that the final measurement will have a higher likelihood of being the period that we seek.
As a circuit we just described doing this:

References
[1] Cleve, Ekert, Macchiavello, Mosca – Quantum algorithms revisited, Proceedings of the Royal Society 454 (1998).
[2] Nielsen, N. & Chuang, I. L. – Quantum Computation and Quantum Information, Cambridge University Press, (2010).
[3] Kendon, V. M. & Munro, W. J. – Entanglement and its Role in Shor’s algorithm, arXiv:quant-ph/0412140 (2006).
[4] Jozsa, R. – Quantum factoring, discrete logarithms and the hidden subgroup problem, arXiv:quant-ph/0012084 (2001).
[5] Cleve, R., Ekert, A., Macchiavello, C., & Mosca, M., – Quantum Algorithms Revisited, (1997)
